立体 の 表面積 と 体積 196311

面積の公式はπ r 2 なので、 π r 2 ＝36π r ＝6（cm） 半径＝6cmなので、 直径は、6×2＝12（cm） ≪答≫ 12cm ※水面の半径を求めてからも解けるから試してみてね！ ＜前： L37 相似な立体の表面積と体積の比 の問題 『第5章 図形と相似』の復習テスト の問題数学16章空間図形「立体の表面積と体積」＜準備問題①＞ 組 番 名前 面積や体積の表し方や求め方について，次の問いに答えなさい。 （1）次のア～ウの面積を求めなさい。 （1マス1㎝の方眼で，イの縦の長さは05㎝とする。） ア イ ウ 1㎝2 よって求める立体の体積＝256＋64＝3（cm³） ～別解～ 求める立体の体積＝384－64＝3（cm³）となります。 答え 3cm³ ～立体の体積・表面積の求め方～ 円柱の体積の求め方公式 円柱の表面積の求め方公式 三角柱の体積の求め方公式 円錐の体積

５章３節２ 相似な立体の表面積や体積の比 数学のすすめ

立体 の 表面積 と 体積

立体 の 表面積 と 体積-ここからは体積を学んでいきたいと思います。体積は表面積と違って簡単です！ 公式があるのでしっかり覚えていきましょう！単位が「cm²」ではなく「cm³」なので注意してください。 「柱の体積＝底面積×高さ」 で求めることができます。ちなみにこれを\(R\)で微分すると、表面積の\(4\pi R^2\)になります。 それは後ほど明らかになるでしょう。 (3B)微小面積（体積）を幾何学的に計算して積分する方法

中1 数学 中1 立体の体積 Youtube

小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題 球の表面積の公式はおぼえられた？？ 9匹（球）のヒョウ（表面積）の捕獲に失敗（4π）したあるじ（rの二乗） という語呂さえおぼえておけば大丈夫。 表面積と体積の公式をごっちゃまぜにすることなんてないはずだよ。 がんばって暗記してみてね^^ そんどっちが体積で、どっちが表面積だっけ？ というようにごちゃごちゃになっちゃう人も多いです。 そういう人は、 体積と表面積の単位に注目しましょう。 体積の単位には\(cm^3\)、\(m^3\)というように3乗がついているよね。

47 7 立体の体積と表面積 133 次の図の直方体の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 137 次の図の立体の体積と表面積を求めよ。 ⑴ ⑵ 135 次の図の円柱の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 134 右 の図は ，円柱とその展開図である。 次の問いに答えよ。求める体積は ＝352cm 3 。 表面積 直方体2本の表面積は （4×4×212×4×4）×2 ＝448cm 2 。 重なっている表面積は 4×4×22×4×4＝64cm 2 。 求める表面積は＝384cm 2 。立体の表面積と体積 表面が、平面や円、球などを含む \(3\) 次元の空間的な広がりをもつ立体において、その表面の面積を合わせたものを表面積といいます。

立体の体積を求めるには，体積の微分が断面積になることを利用します． すなわち，左端 a から座標 x までの区間にある体積を x の関数として V (x) で表し， x における断面積を S (x) とおきます． 上で復習した面積の求め方と同様にして ⊿V (x)≒S (x)⊿x弓形の回転体の体積と底面積と表面積を計算します。 一部が欠けた弓形の回転体の体積 一部が欠けた弓形の回転体の体積 弓形の回転体を切断した体積と表面積を計算します。 半球台の体積 半球台の体積 半球台の半径と高さから体積と表面積を計算します。 立体の体積の求め方（公式）を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。 体積の求め方公式 立方体・直方体の体積の求め方 円柱の体積の求め方 三角柱の体積の求め方 円錐の体積の求め方 四角錐の体積の求め方 注意 スポンサードリンク (adsbygoogle

複雑な体積 表面積の問題 家庭教師としの勉強部屋

中１数学 円柱の体積 表面積はどうやって求めるの まなビタミン

立体の体積 角柱、円柱の体積 柱の体積 = 底面積 × 高さ (例) 三角柱 高さ8cm 底面積 5cm 2 体積=5×8=40 四角柱(直方体) 4cm 3cm 8cm 底面積=4×3=12 体積=12×8=96 半径5cm 高さ 8cm 円柱 底面積=5×5×π=25π 体積=25π×8=0π 例題次の立体の体積を求めよ。 底面積15cm 2, 高さ6cmの五角柱 底面の半径2cm, 高さ10cm〇〇錐という立体の体積は底面積×高さ×\(\frac{ 1 }{ 3 }\)と覚えている方も多いと思いますが、\(\frac{ 1 }{ 3 }\)という係数はここの導出過程から出てくるものです。 球 最後に球の体積についてです。半径\(R\)の球の体積を求めてみたいと思います。立体は円柱になり，表面積は底面積×2=16 π ×2 (cm 2 )と側面積8 π ×7 (cm 2 )の合計になります 底面積2つで32 π (cm 2 )，側面積56 π (cm 2 )の合計は π (cm 2 ) (答) ※以下，8番以後の問題を解くには，中学校3年生で習う三平方の定理が必要になります．まだ習っ

円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題

中学生の問題です 答えを見ても理解できなかったので解説お願いし Yahoo 知恵袋

底面の周： 6π(cm) 6 π ( c m) 表面積：「底面積×2底面の周×高さ」より、 9π ×2 6π× 7＝60π(cm2) 9 π × 2 6 π × 7 ＝ 60 π ( c m 2) 体積は63cm3 63 c m 3 、表面積は60cm2 60 c m 2 ちなみに角柱・円柱の体積や表面積について、自由に印刷できる練習問題を用意しました 立体図形の総合問題（桜蔭中学 13年） 円すいを切った体積（大妻中学 13年） 長さ比と体積比は？（開成中学 過年度） 残った立体の体積は？（早稲田中学 14年） 表面積と体積は？（明星中学 10年） この立体図形の体積は？ うさぎでもわかる解析 Part27 2重積分の応用（体積・曲面積の求め方） 19年11月4日 21年7月16日 49分1秒 ももうさ スポンサードリンク こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積（表面積）を求める方法についてまとめてい

2

立体の表面積と体積 の問題のわからないを5分で解決 映像授業のtry It トライイット

表面積は「24」になってますね。 すなわち、体積が8倍になっても、表面積は8倍の「64」にはならないことが分かります。 ×体積8 ： 表面積48 ではなく、 体積8 ： 表面積24 という比です。 水って形は変わっても体積は変わらない 以上！ 次回は表面積の問題のコツを解説します。 基本となる考え方から、円錐の表面積を深く理解するところまで、ポイントをしぼってお伝えしていきます。 next→中学数学「平面図形」④ 表面積の問題のコツ 積み重ねられた立体の体積：立体を段ごとに分解 最初は自分で図を描いてみても良いです。 125 260 180＋108＋45＝333 125＋260＋333＝125＋593＝718 答え）718cm 3 （2）この立体の表面積を求めなさい 積み重ねられた立体の表面積：（前＋右＋上）×2 97＋97＋111

円柱を2つ重ねた立体の表面積の求め方 Qikeru 学びを楽しくわかりやすく

角柱 円柱の表面積と体積の公式 数学fun

この立体について以下の問いに答えなさい。 1 表面積を求めなさい。 2 ＝81π ≪球面の面積≫ 2 ）× 240 360 ＝216π 81π＋216π ＝297π ≪答≫ 表面積：297πcm 2 2 体積を求めなさい。 三角柱の体積の求め方は 「底面積 × 高さ」でしたね。 底面積は 4 × 4 × 1 2 = 8 よって、三角柱の体積は 8 × 8 = 64 体積は 64（ c m 3 ） となります。 続いて、 三角柱の表面積の公式は 「底面積 × 2 側面積」でしたね。 すると、底面積は先に求めた 8 c m 2 立体図形の切り口（浦和明の星中学 受験算数問題 09年） 立体の表面積と体積（中学受験 算数入試問題） 重なった三角柱（中学受験算数 立体図形） 表面積と体積は？ （中学受験算数 頭の中で回してみた問） 面積の差は？ （中学受験算数 難しく考え

円柱の表面積と体積を求める公式 具体例で学ぶ数学

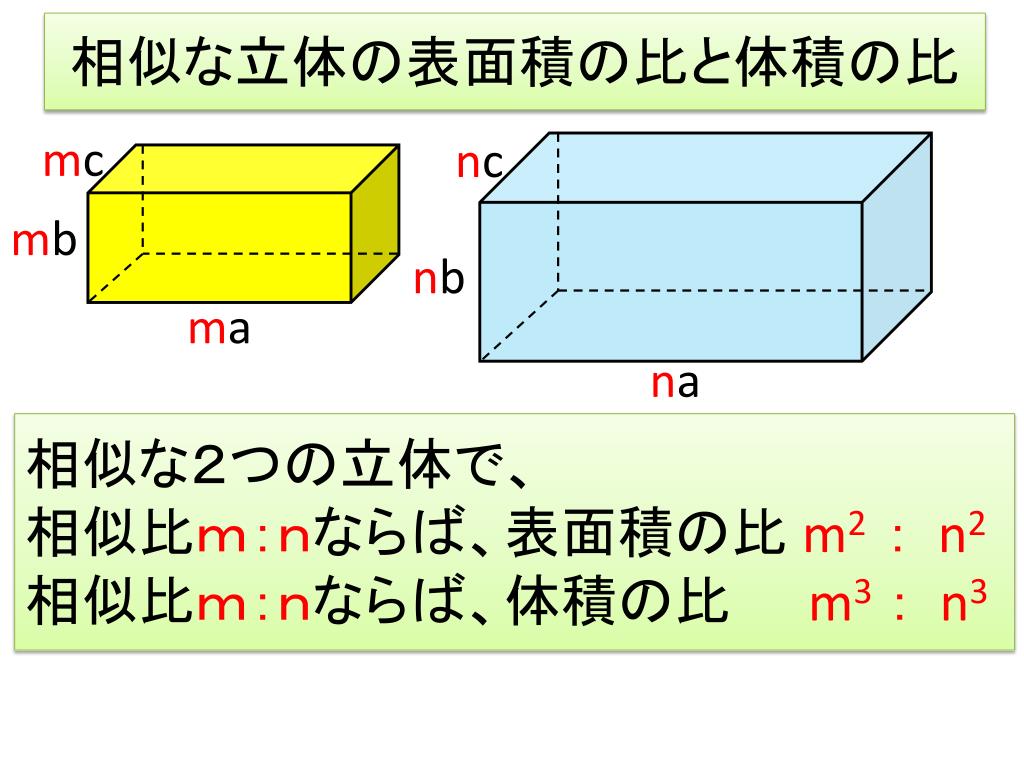
Ppt 相似な立体の表面積 体積 Powerpoint Presentation Free Download Id

体積 (たいせき) とは、 立体 (りったい) が 空間 (くうかん) の中で 占 (し) める大きさのことです。 このページでは、 様々 (さまざま) な立体の体積の 求 (もと) め方を 一覧 (いちらん) にまとめています。 図形 (ずけい) と体積の 公式 (こうしき) をセットで 覚 (おぼ) えましょう！

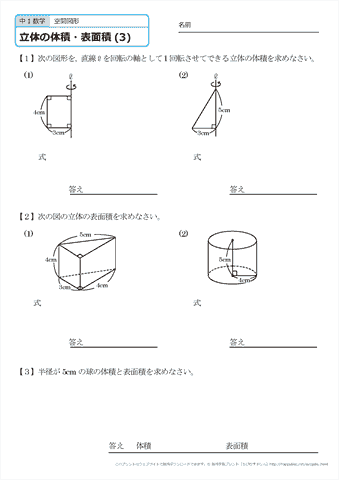
中学１年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学

中1 数学中2 立体の体積と表面積 公式 中学生 数学のノート Clearnote

球の体積と表面積 公式と計算問題と証明 Irohabook

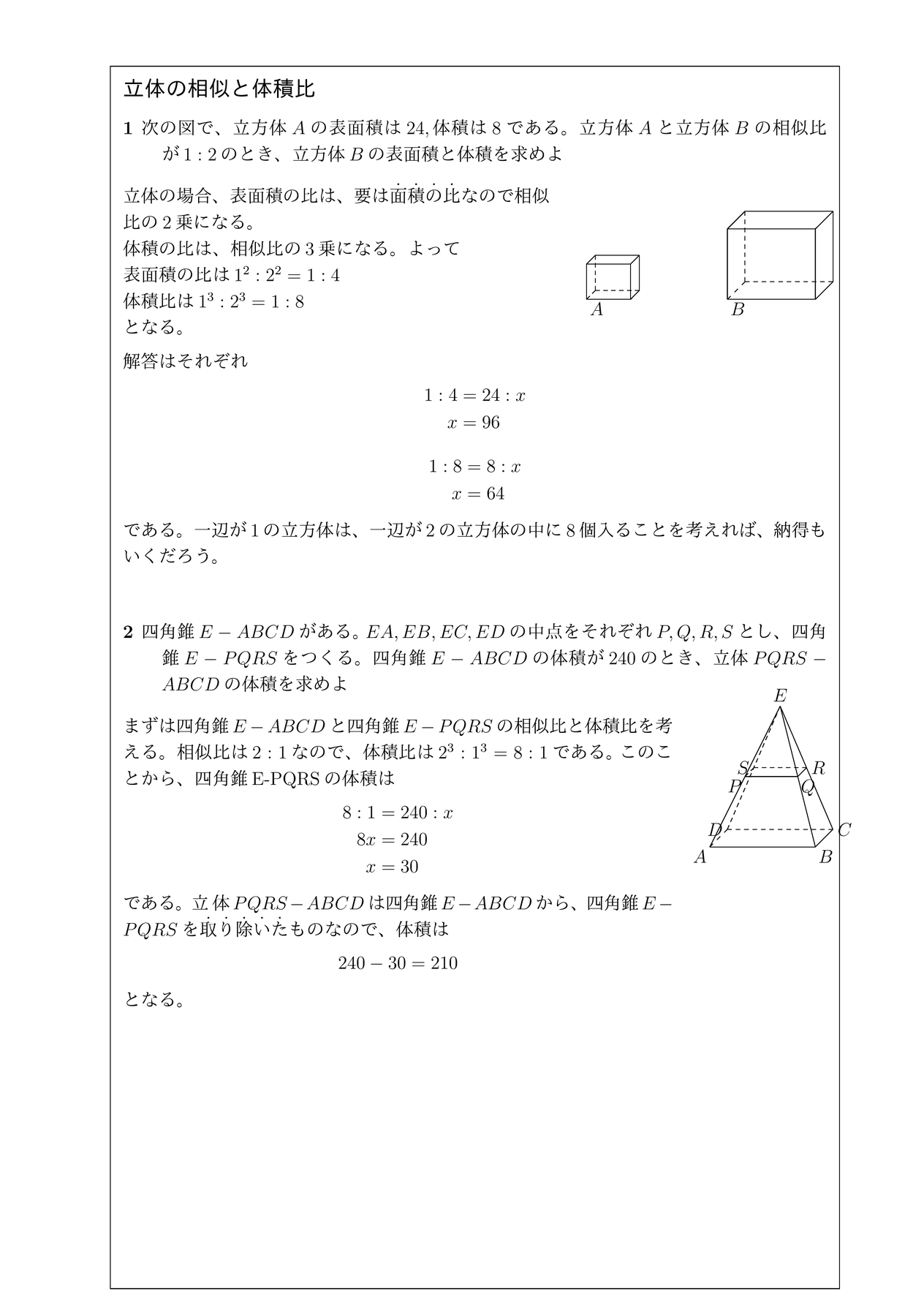
立体の相似と表面積比 体積比 チーム エン

角錐 円錐の体積と表面積の公式 数学fun

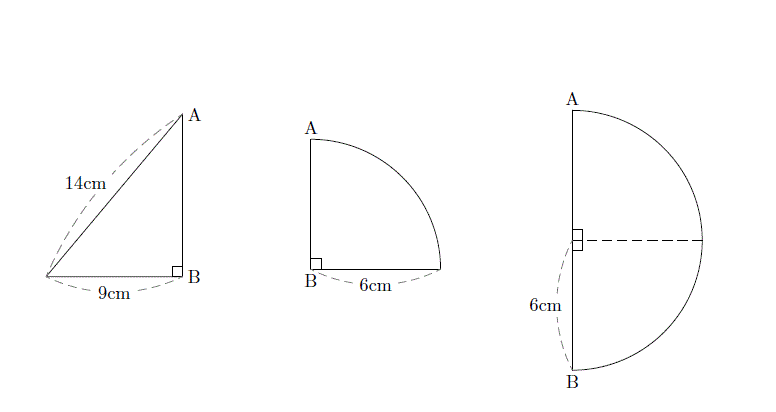
かみのドリル 立体の体積と表面積 回転

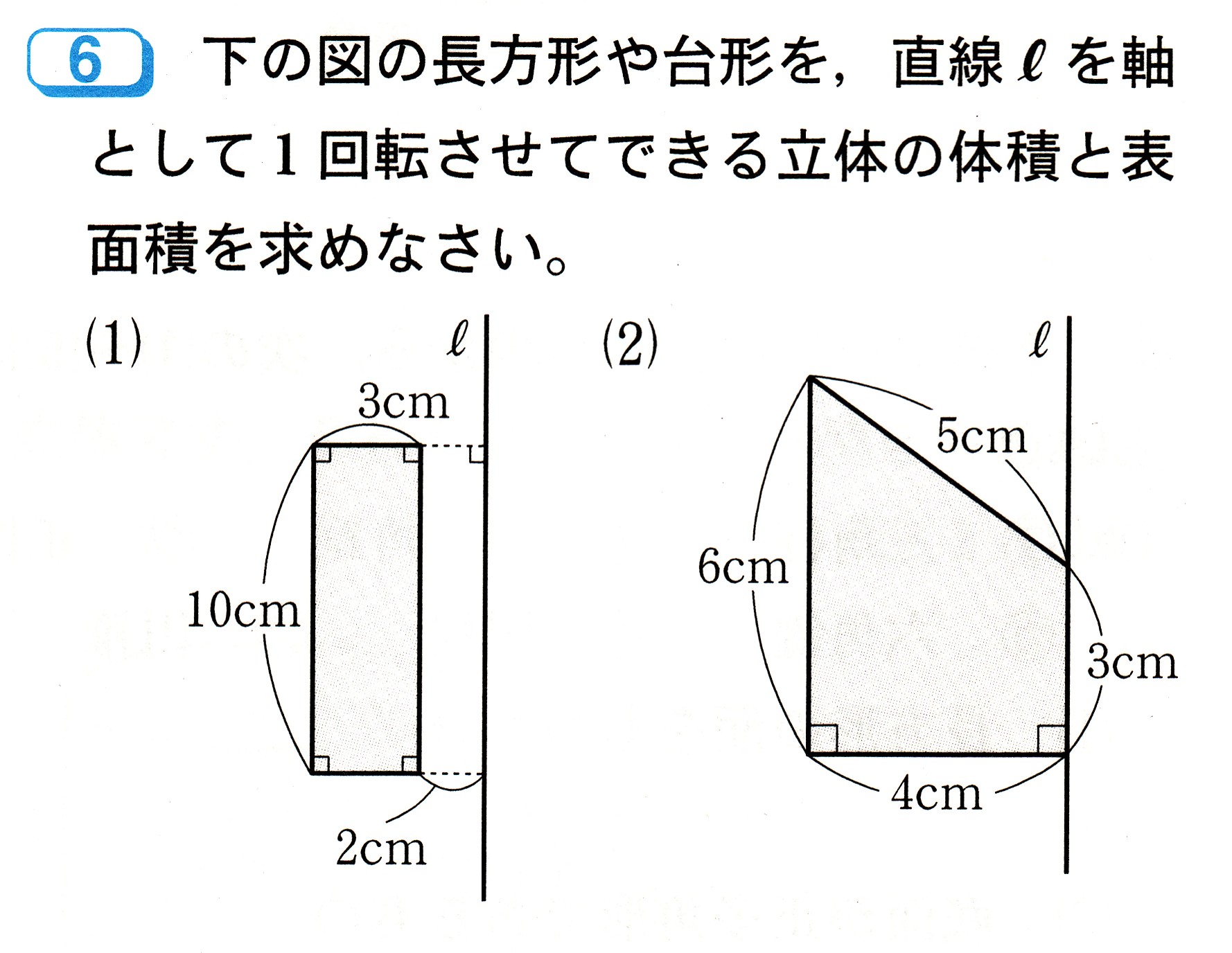
中学1年数学 立体の表面積と体積 確認問題６ あんのん塾

完全個別指導塾ceeds 立体図形の体積や表面積を 求める問題に挑戦する 小5の生徒さん Facebook

立体の体積と表面積 １ 柱体の表面積

立体の表面積と体積 わかる数学

立体の表面積

立体の表面積と体積2

中1 数学 中1 立体の体積 Youtube

中1 中1数学 空間図形 体積と表面積の公式一覧 中学生 数学のノート Clearnote

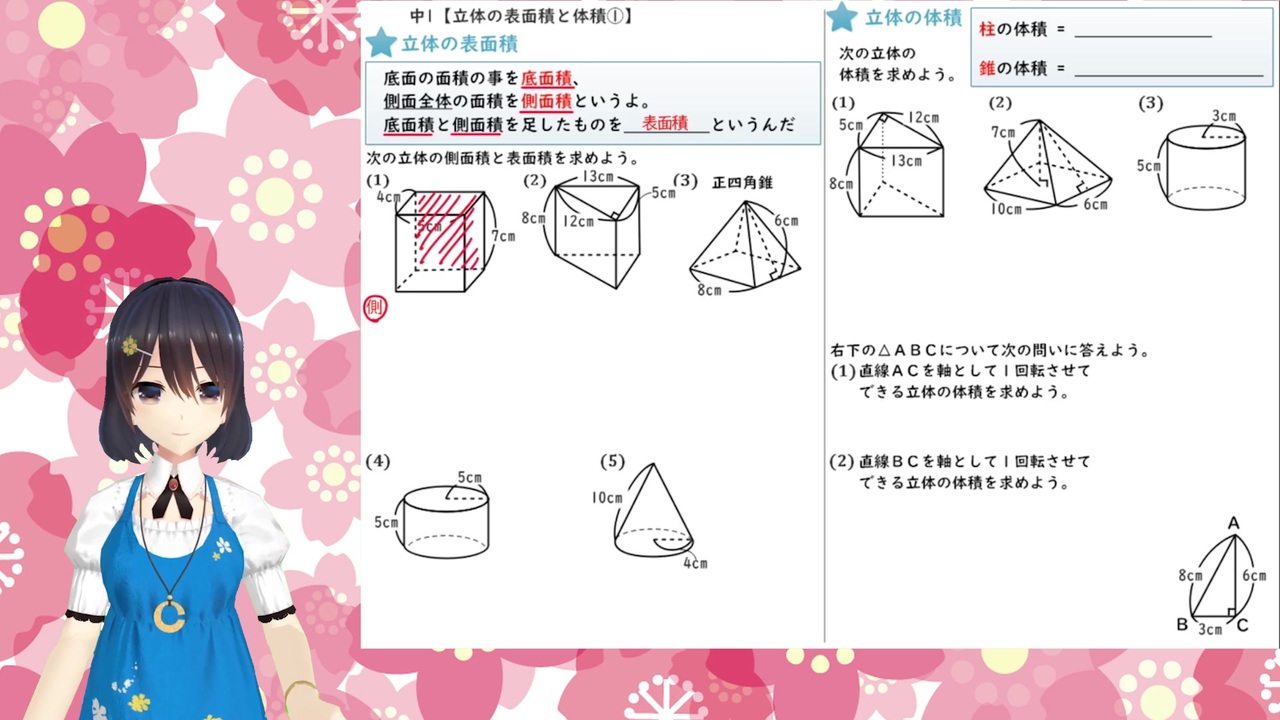
数学 中学1年 立体の表面積と体積 ニコニコ動画

3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ

立体の表面積と体積 の問題のわからないを5分で解決 映像授業のtry It トライイット

3

公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ

５章３節２ 相似な立体の表面積や体積の比 数学のすすめ

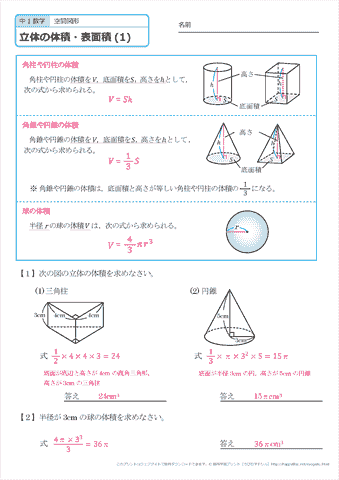
中学１年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

1

立体図形の体積や表面積 新学習指導要領小学校算数科のキーワード Amazon Com Books

三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ

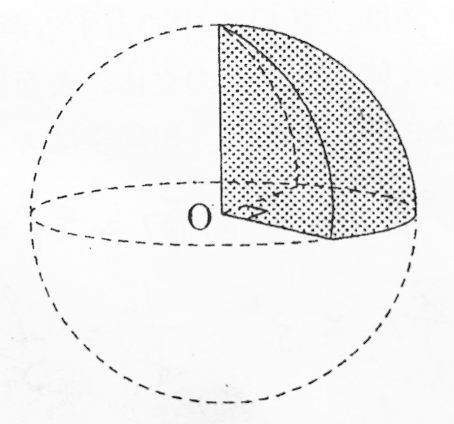
球の問題 苦手な数学を簡単に

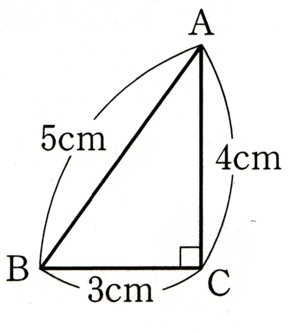
中学1年数学 立体の表面積と体積 練習問題4 解答 解説 あんのん塾

1

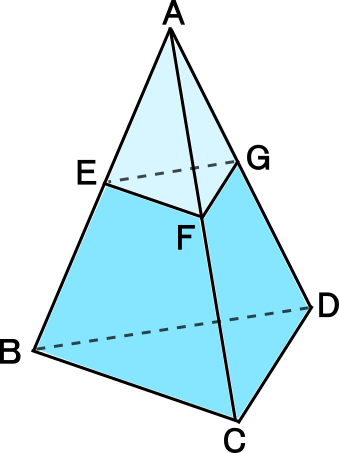
中学３年数学練習問題 相似な立体の表面積と体積の比 図形と相似

算数の問題です 1 図の立体は 円柱を半分に切った形です この立体の体積は何 Yahoo 知恵袋

6 16 6章 空間図形立体の表面積と体積 角錐の表面積 フロントエンドなブログ

1

Ppt 相似な立体の表面積 体積 Powerpoint Presentation Free Download Id

円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ

Studydoctor柱体や角錐の表面積の求め方 中学１年数学 Studydoctor

中1 中1 数学まとめ 立体の体積や表面積など 中学生 数学のノート Clearnote

三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学

高校入試 英語 数学 学習 立体の表面積と体積

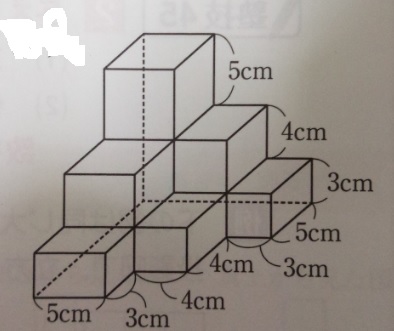
積み重ねられた立体 表面積と体積 中学受験 塾なし の勉強法

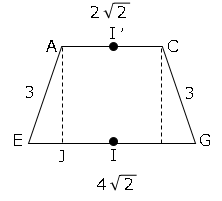
立体の表面積と体積9 数学の要点まとめ 練習問題一覧

立体の表面積と体積 数学の要点まとめ 練習問題一覧

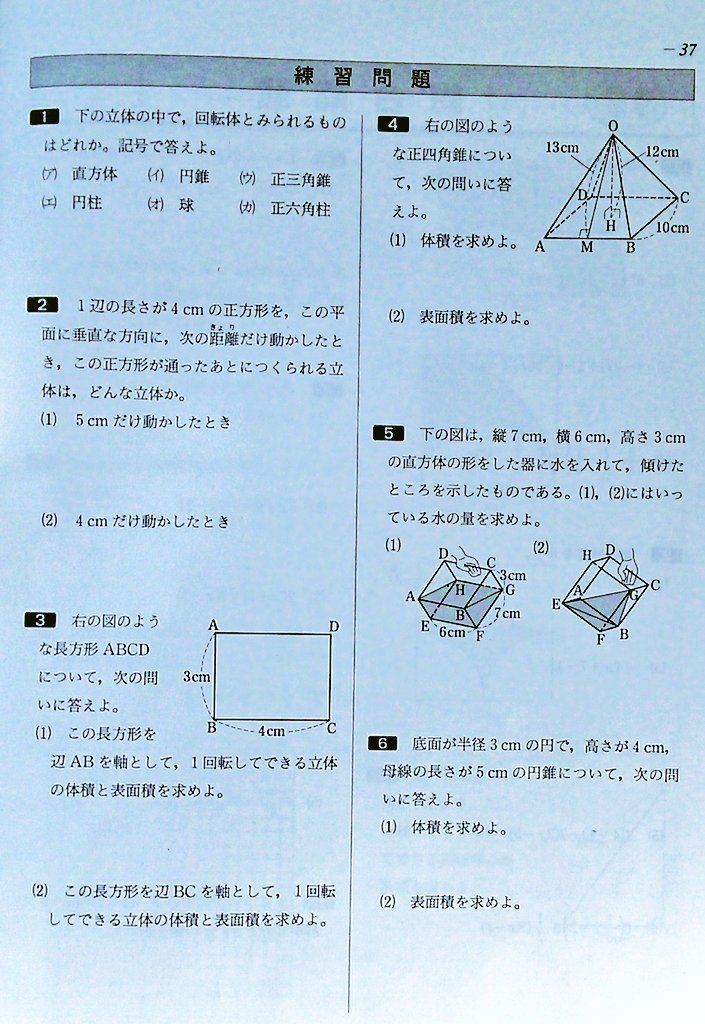
立体の体積と表面積

うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾

実際にやってみました 聖徳大学附属取手聖徳女子中学校 高等学校

数学 中学1年 立体の表面積と体積 ニコニコ動画

本時の目標 身近な直方体をもとに実際に表面積と体積を求めることで 相似な立体の表面積比と体積比について理解する Ppt Download

立体の体積と表面積 Ict教材eboard イーボード

球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典

５章３節２ 相似な立体の表面積や体積の比 数学のすすめ

１つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード

無料 中１数学 標準問題 解答プリント 143 空間図形６ 立体の体積

中1 数学 中1 立体の表面積 Youtube

複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座

6 17 第6章 空間図形立体の表面積と体積 円錐の表面積 しもじまのネタ帳

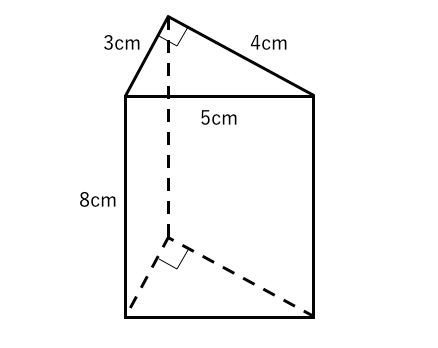
立体の表面積を求める 練習問題 苦手な数学を簡単に

立体の表面積

中1数学 立体の表面積と体積の求め方と練習問題 Pikuu

円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者

球の表面積と体積の公式 数学fun

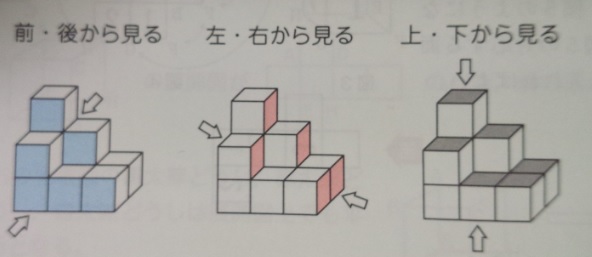
積み重ねられた立体 表面積と体積 中学受験 塾なし の勉強法

１つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード

中１数学 円柱の体積 表面積はどうやって求めるの まなビタミン

3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ

表面積の求め方 計算公式一覧

10 面積比 体積比 球の表面積と体積

21年 千葉県公立高校入試 数学 第2問 ３ 円柱の体積 表面積 配点5点 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト

角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学

立体の表面積と体積 中学受験 算数入試問題 どう解く 中学受験算数

表面積と体積の比の問題 立体の相似比を出すのが一番最初だ 中学や高校の数学の計算問題

体積 表面積

回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

中3数学 図形と相似34 相似な立体の表面積比 体積比 すべて無料 星組の中学数学講座

ウチダ 教材総合カタログ 中学校

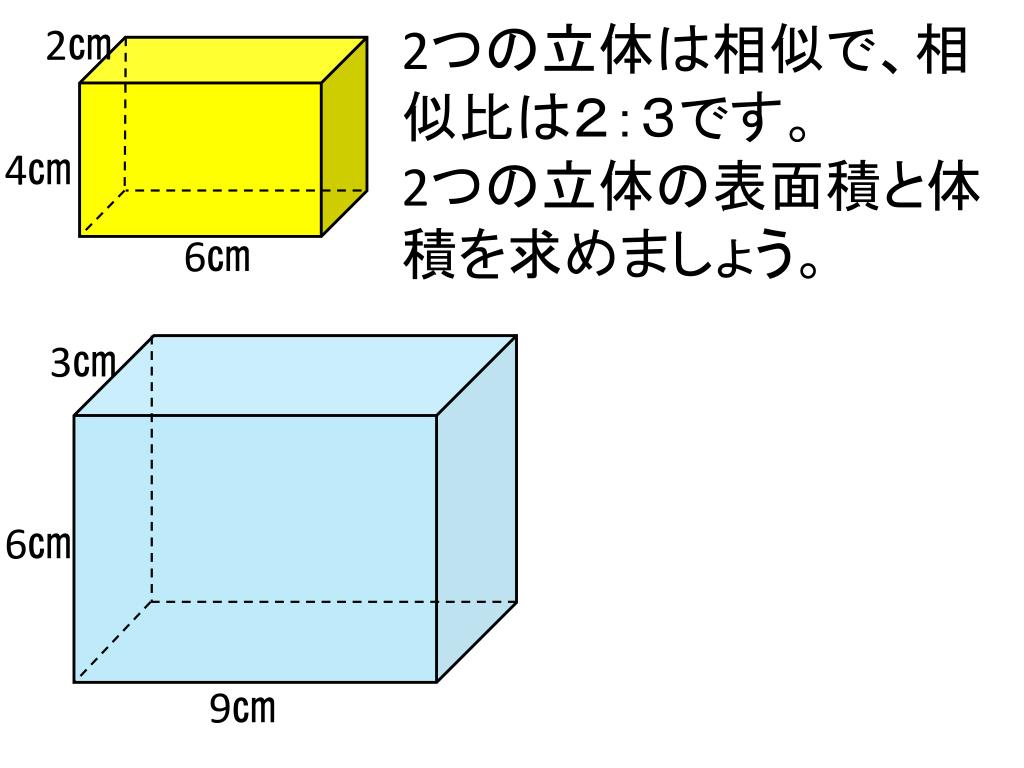
Ppt 相似な立体の表面積 体積 Powerpoint Presentation Free Download Id

中1数学 立体の表面積と体積の求め方と練習問題 Pikuu

無料 中１数学 基本問題 問題プリント 空間図形６ 立体の体積 143

高校入試 英語 数学 学習 立体の表面積と体積

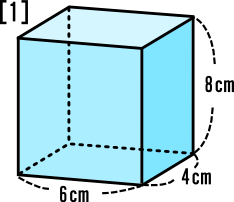
中学１年数学練習問題 立体 円柱 三角柱 四角錘等 の表面積の問題

表面積の求め方 計算公式一覧

中学１年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

立体の表面積と体積 わかる数学

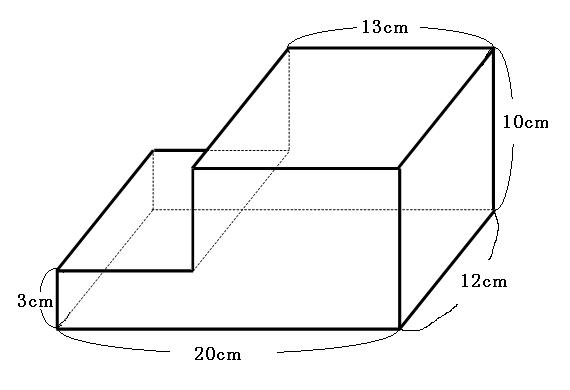
立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか

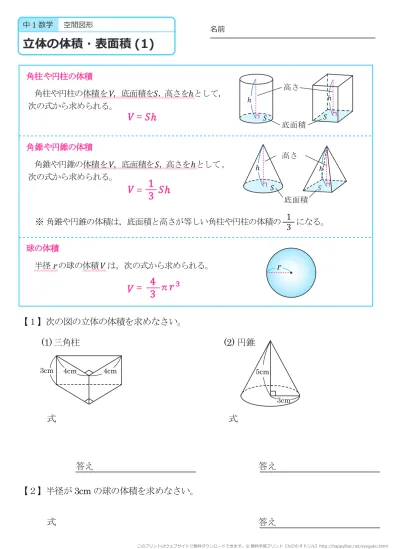
中学１年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 このページの答えのプリント 全部

入試問題 算数3問目

円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者

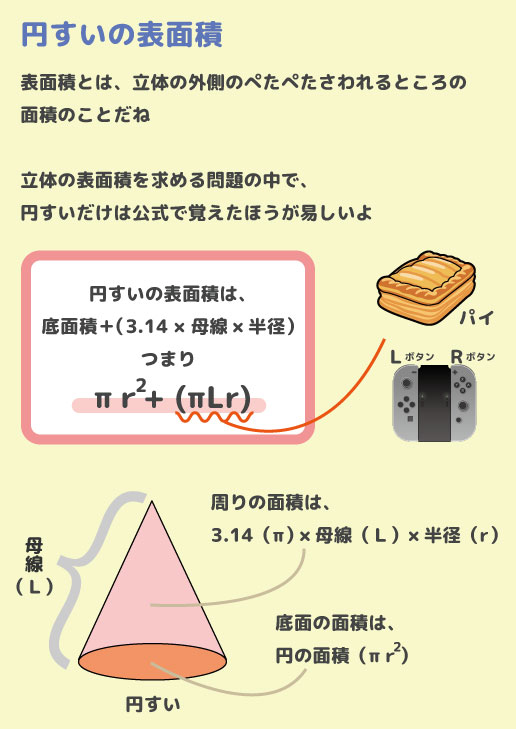
中１数学 すい体の体積と円すいの表面積 数学検定５級 お家でお勉強

角錐 円錐の体積と表面積の公式 数学fun

Gajiansejutadollarulhw いろいろ 立体 の 表面積 と 体積

中1数学 立体の体積と表面積 教科書p194 5 3学期期末テスト 赤城 ᐡᐤᐡ

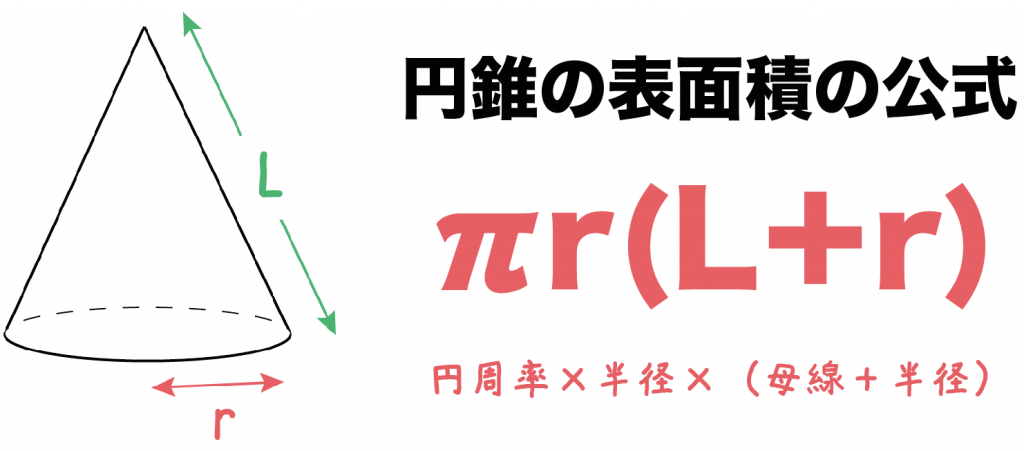
計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

中１数学31 立体の表面積と体積 Youtube

立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム